スーパームーン

2021年5月26日はスーパームーンと月食が同時に見える貴重な機会でしたが，残念ながら雲に覆われたために私の自宅（大阪）からは観測することはできませんでした．みなさんの地域ではどうでしたか？できればその様子を動画におさめたいと準備もしていましたが，まったくの空振りに終わってしまいました．

2020年4月に撮影した満月の写真

（今回のスーパームーンではありません）

せっかくですので，今回はスーパームーンに焦点を当てた学習を考えてみましょう．

スーパームーンとは「満月としては1年で最も地球に近くなる日の月」だということですが，言い換えれば満月でも遠くになることもあるということです．当然，そこから月の公転軌道が楕円であることに気づかせる学習ができるでしょう．

しかし，月の公転軌道が楕円だとしても，実際にどのような楕円かは人によって認識が異なるはずです．

ここでみなさんに質問ですが，月の公転軌道は下のア～エのうちどの形に近いと思いますか？ただし，アは真円で楕円ではありません．

それでは確かめてみましょう．まず，楕円の定義から調べてみると，楕円は「平面上のある２定点からの距離の和が一定となるような点の集合」です．この定義にある２つの定点を焦点と呼びます．この焦点は楕円の中心から同じ距離にある2点と決まっています．図で表すとこのようになり，A-B間の距離+B-C間の距離を一定に保った状態でB点を移動させたときにB点が描く線が楕円となります．

このことからすれば，楕円の長半径と楕円の中心から焦点までの距離が決まると，月の公転軌道を具体的に描くことができます．

あとは，実際の月の公転軌道の長半径とその中心から焦点までの距離がわかればよいのですが，今回は楕円の形を知りたいので，その比率から求めることにします．（長半径の長さ）分の（楕円の中心から焦点までの長さ）を離心率といいますが，この値はネットなどで検索すればすぐにわかります．月の離心率は，約0.055です．

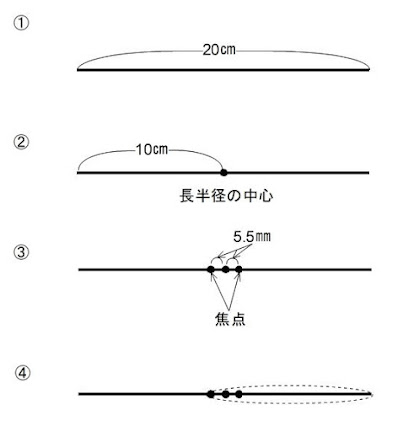
それではこの離心率を使って，月の公転軌道を描いていきましょう．まず①20㎝の直線をひきましょう．そして，②真ん中の10㎝のところに点を打ちましょう．これが楕円の中心です．次に焦点を決めましょう．離心率が0.055であることから，③楕円の中心から両側に5.5㎜離れた点を打ちましょう．これが２つの焦点です．そして，この２つの焦点に押しピンを突き刺してください．④ピンと張った状態で，左側の押しピンと20㎝の直線の右端まである糸の輪をつくり，20㎝の直線の右端をスタートとして，糸をピンと張ったままペンを動かしてみてください．描いたペンの跡が月の公転軌道を表しています．そして，この時の片方の焦点の位置が地球の位置となります．

私が月の公転軌道を描いた時の動画を下に貼り付けておきます．やり方がわからない人は参考にしてみてください．

いががだったでしょうか？自分が思い描いていた楕円とは違ったと感じた人がいたことでしょう．「何だ！ほとんど真円なのか？」と思って終わることは簡単かもしれませんが，地球からの観測結果だけに基づいて，江戸時代の初めごろにはこのような微妙な差に気づいていたケプラーには驚かされます．ただし，ケプラーが最初に発見したのは火星の公転軌道が楕円だということです．火星の離心率は月のそれよりは大きいことから，月よりもわかりやすかったでしょうが，火星の公転軌道も結構真円に近いものです．興味のある人は書いてみてください．火星の離心率は0.093です．